00. 인공 뉴런: 초기 머신러닝의 간단한 역사
- 맥컬록-피츠(MCP): 1943년 워렌 맥컬록과 월터 피츠가 처음으로 간소화된 뉴런 개념
- 뉴런
- 뇌의 신경세포와 서로 연결되어 있음
- 화학적/전기적 신호를 처리하고 전달하는데 관여
- 신경 세포를 이진 출력을 내는 간단한 논리 회로로 표현한 것
- 수상 돌기에 여러 신호가 도착하면 세포체라는 한 곳으로 모아짐
- 합쳐진 신호가 특정 임계 값을 넘으면 출력 신호가 생성되고 축삭 돌기를 이용하여 전달됨
- 뉴런
- 퍼셉트론 학습: 프랑크 로젠 블라트가 MCP 뉴런 모델을 기반으로 발표
- 자동으로 최적의 가중치를 학습하는 알고리즘
- 이 가중치는 뉴런의 출력 신호를 출력할 지 결정하기 위해 입력 특성에 곱하는 계수
- 새로운 데이터 포인트가 한 클래스에 속하는지 예측할 수 있음
01. 인공 뉴런의 수학적 정의
- 인공 뉴런(artificial neuron) 아이디어를 두 개의 클래스가 있는 이진 분류(binaray classification) 작업
- 두 클래스는 양성 클래스(1)과 음성 클래스(-1)로 나눠짐
- 입력 값 x와 상응하는 가중치 벡터 w의 선형 조합으로 결정 함수를 정의함
- 최종 입력은 각각의 가중치 * 벡터의 합
- 특정 샘플의 최종 입력이 사전에 정의된 임계 값보다 크면 양성 클래스(1), 작으면 음성 클래스(-1)로 예측
- 퍼센트론에서의 결정 함수: 단위 계단 함수(unit step function)
- 절편: 머신러닝 분야에서의 음수 임계 값
- 전치(transpose): 첨자 T 의미, 열 벡터를 행 벡터 또는 그 반대로 바꾸는 행위
- 행렬에 적용하여 대각 원소를 기준으로 반전시킬 수 있음

02. 퍼셉트론 학습 규칙
- 환원 주의(reductionism) 접근 방식: 뇌의 뉴런 하나가 작동하는 방식
- 출력을 내거나 내지 않는 두 가지 경우만 존재
- 퍼셉트론 알고리즘 요약
- 가중치를 0 또는 랜덤한 작은 값으로 초기화
- 각 훈력 샘플 x(i)에서 다음 작업 진행
- 출력 값을 계산(출력 값: 앞서 정의한 계단 함수로 예측한 클래스 레이블)
- 가중치 업데이트
- 전체 가중치에 대한 가중치 업데이트 값을 계산할 때 이용하는 것: 학습률(0.0~1.0), 훈련 샘플의 진짜 클래스 레이블, 예측 클래스 레이블, 훈련 샘플
- 중요: 가중치 벡터의 모든 가중치를 동시에 업데이트, 즉 모든 가중치가 각자의 가중치 업데이트 값에 의해 업데이트가 되기 전에 예측 레이블을 다시 계산하지 않음
- 정확히 예측한 경우: 가중치 변경 없이 그대로 유지(업데이트 값이 0)
- 잘못 예측한 경우: 가중치값이 양성 또는 음성 클래스 방향으로 이동
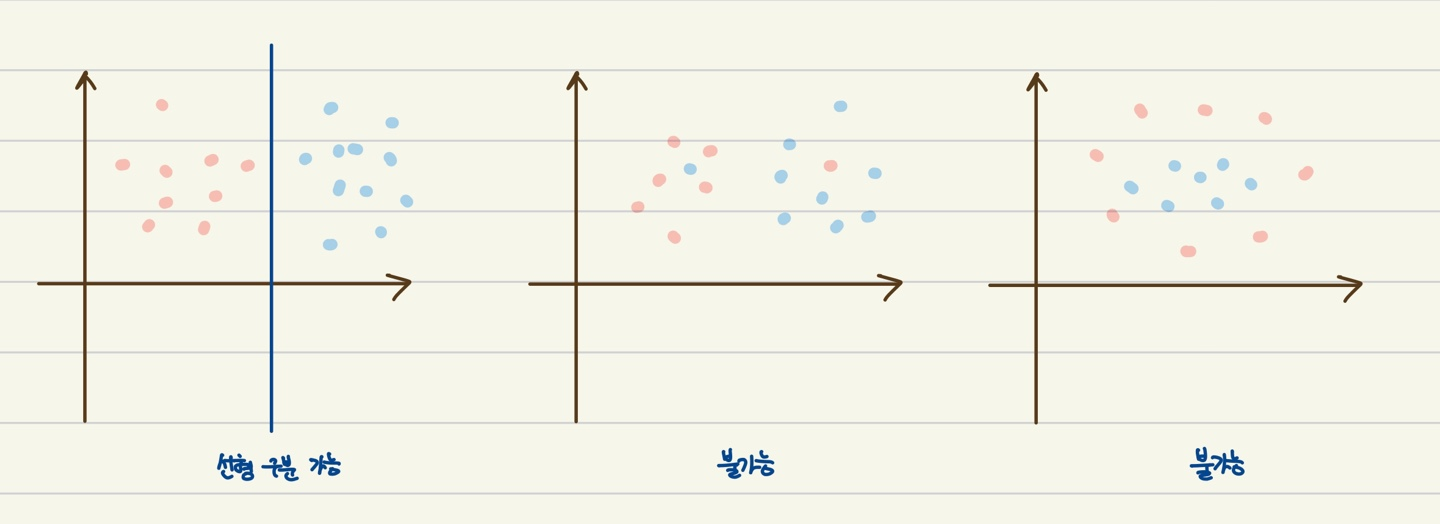
- 퍼셉트론이 정확하게 적용되는 경우: 두 클래스가 선형적으로 구분되고 학습률이 충분히 작은 경우에 수렴이 보장
- 두 클래스를 선형 결정 경계로 나눌 수 없을 경우: 훈력 데이터 셋을 반복할 최대 횟수, 즉 에포크(epoch)를 지정하고 분류 허용 오차를 지정할 수 있음 → 지정하지 않으면 가중치 업데이트가 멈추지 않음

'머신러닝 & 딥러닝' 카테고리의 다른 글
| [머신러닝 & 딥러닝] K-최근접 이웃(K-Nearest Neighbor, KNN) (2) | 2025.04.14 |
|---|---|
| [머신러닝 & 딥러닝] 적응형 선형 뉴런(ADAptive Linear NEuron, ADALINE) (0) | 2025.04.14 |
| [머신러닝 & 딥러닝] 전체적인 작업 흐름 (0) | 2025.02.19 |
| [머신러닝 & 딥러닝] 기본 용어와 표기법 (0) | 2025.02.18 |
| [머신러닝 & 딥러닝] 머신러닝을 시작하기 전에 (0) | 2025.02.13 |