01. 균형 이진 트리 (Balanced Binary Search Tree)
- 모든 노드의 좌우 서브트리 높이가 1이상 차이나지 않는 트리 (이진 탐색 트리)
- 노드의 삽입 / 삭제가 일어나는 경우 균형을 유지하도록 하는 트리
- 종류
- AVL 트리
- Red-Black 트리
02. 이진 탐색 트리의 편향 발생
- case 1) 삽입 순서: 20 → 10 → 30 → 5
- case 2) 삽입 순서: 5 → 10 → 20 → 30
- 이진 탐색 트리의 규칙을 벗어나고 값들의 편향이 발생함

03. AVL 트리
- 노드가 삽입/삭제가 일어나는 경우 트리의 균형을 체크하고 유지하는 트리
- 각 노드의 BF(Balance Factor)를 [1, 0, 1]만 가지게 하여 균형 유지
- BF: (왼쪽 서브 트리 높이) - (오른쪽 서브 트리 높이)
- 앞서 언급한 case 1)과 case 2)의 경우,
- case 1) BF = (왼쪽 서브 트리 높이: 2) - (오른쪽 서브 트리 높이: 1) = 0 (균형을 이루고 있음)
- case 2) BF = (왼쪽 서브 트리 높이: 0) - (오른쪽 서브 트리 높이: 3) = -3 (편향 일어남)
- case 2)의 경우, 리벨런싱 작업 필요
- 앞서 언급한 case 1)과 case 2)의 경우,

04. AVL 트리 - 리밸런싱
- 리벨런싱: 무너진 이진 트리의 균형을 다시 맞춰주는 작업
- 균형이 깨진 경우
- BF가 '+'가 나오면 왼쪽 서브 트리의 문제
- BF가 '-'가 나오면 오른쪽 서브 트리의 문제
- 회전 연산
- 단순 회전: LL, RR
- 이중 회전: LR, RL
05. AVL 트리의 회전 연산
- L과 R의 의미: 노드가 왼쪽으로 치우쳐져 있다면 L, 오른쪽으로 치우쳐져 있다면 R
- ex) LR: 노드들이 위에서 아래 순서대로 왼쪽 방향, 오른쪽 방향으로 편향 문제가 생김을 의미
- 치우쳐져 있지 않은 반대 방향으로 회전 연산을 진행
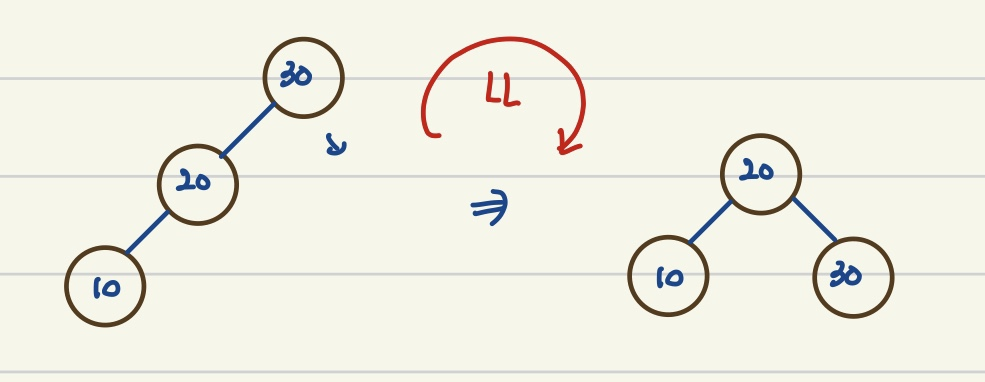
- ex) LL: 왼쪽으로 노드들이 치우쳐져 있으므로 오른쪽 방향으로 회전
- 단순 회전
- LL(Left-Left)
- 회전 1회
- 오른쪽 방향으로 회전
- RR(Right-Right)
- 회전 1회
- 왼쪽 방향으로 회전
- LL(Left-Left)
- 이중 회전
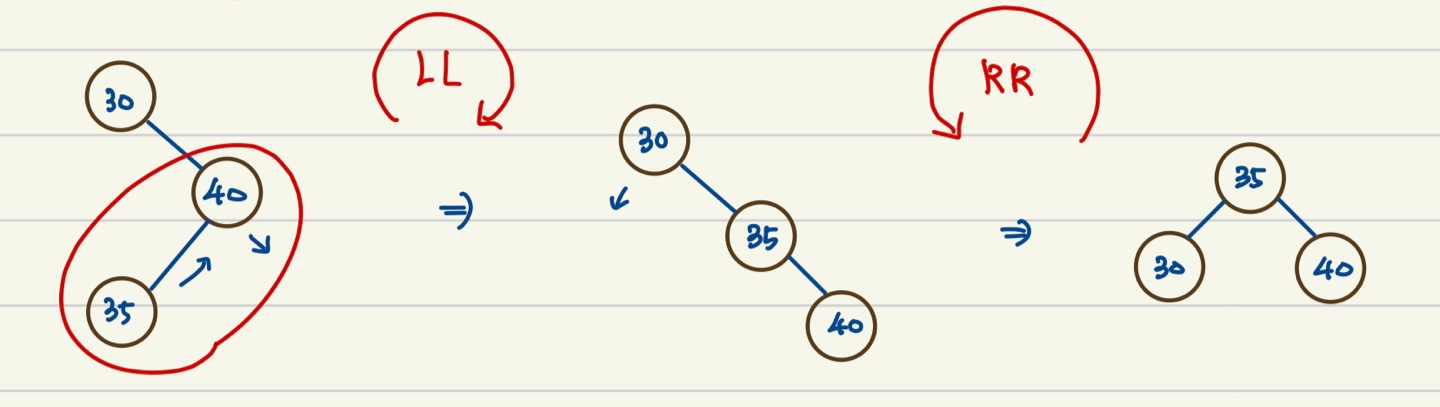
- LR(Left-Right)
- 회전 2회
- RR 회전 후 LL 회전
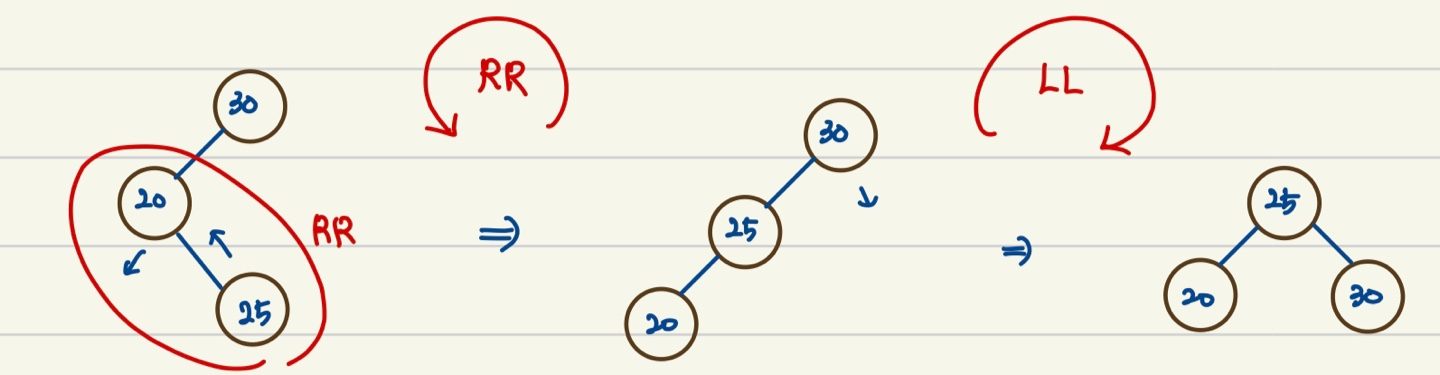
- RL(Right-Left)
- 회전 2회
- LL 회전 후 RR 회전
- LR(Left-Right)

06. JAVA 코드로 구현하기
(1) 노드 구현
class Node{ //데이터를 저장하는 노드 객체
int key; //값 저장하는 변수
int height; //노드의 높이를 저장하는 변수
Node left; //현재 노드의 왼쪽 노드 정보 저장
Node right; //현재 노드의 오른쪽 노드 정보 저장
// 생성자 - 설정
public Node(int key, Node left, Node right) { //생성자
this.key = key;
this.height = 0;
this.left = left;
this.right = right;
}
}(2) 트리 구현 / 노드 추가 기능
// 트리 구현
class AVLTree {
Node head; //트리의 헤드 노드 저장 변수
// 높이 계산하는 함수
public int height(Node node){
if(node == null){ //null값 들어오면
return -1;
}
return node.height;
}
/*
* Node node: 중간 노드
*/
// LL회전 시 - 오른쪽으로 회전
public Node rightRotate(Node node){
Node lNode = node.left; //중간 노드(node)의 왼쪽 노드를 저장
node.left = lNode.right; //중간 노드의 왼쪽 위치에 중간 노드로 변경
lNode.right = node; //왼쪽 노드의 오른쪽 자식 위치에 중간 노드 위치시킴
//height 업데이트, 둘 중 높은 높이+1
node.height = Math.max(height(node.left), height(node.right))+1;
lNode.height = Math.max(height(lNode.left), height(lNode.right))+1;
return lNode; //왼쪽 자식을 반환시켜서 위로 올라가게 함
}
// RR회전 시 - 왼쪽으로 회전
public Node leftRotate(Node node){
Node rNode = node.right; //중간 노드의 오른쪽을 저장
node.right = rNode.left; //중간 노드의 오른쪽 위치에 중간노드로 변경
rNode.left = node; //오른쪽 노드의 왼쪽 자식 위치에 중간노드를 위치시킴
node.height = Math.max(height(node.right), height(node.left))+1;
rNode.height = Math.max(height(rNode.right), height(rNode.left))+1;
return rNode; //오른쪽 자식을 반환시켜 위로 올라가게 함
}
// LR회전 시 - 왼쪽으로 회전 후, 오른쪽으로 회전
public Node lrRotate(Node node){
node.left = leftRotate(node.left); //왼쪽 회전 후
return rightRotate(node); //오른쪽으로 회전하여 나온 노드를 위로 올라가게 함
}
// RL회전 시 - 오른쪽으로 회전 후, 왼쪽으로 회전
public Node rlRotate(Node node){
node.right = rightRotate(node.right); //오른쪽 회전 후
return leftRotate(node); //왼쪽으로 회전하여 나온 노드를 위로 올라가게 함
}
// 높이 차를 계산하는 기능: (왼쪽 노드의 높이) - (오른쪽 노드의 높이)
public int getBalance(Node node){ //높이차
if(node == null){
return 0;
}
return height(node.left) - height(node.right);
}
// 값을 넣는 기능
public void insert(int key){
this.head = insert(this.head, key); //노드를 반환받아 헤드를 변경(자동 균형 유지)
}
// 값을 헤드에서 부터 비교해가며 넣을 자리를 마련하고, 자동으로 균형을 유지하기 위해 높이차를 계산하며 진행
private Node insert(Node node, int key){
if(node == null){ //null값인 경우: 헤드에 null값을 가진 노드를 저장함
return new Node(key, null,null);
}
if(key == node.key){ //값이 이미 존재할 경우: 중복 허용하지 않음
System.out.println("Already Data: "+key);
return node;
}
if(key < node.key){ //값이 노드보다 작은 경우: 왼쪽 자식으로 이동
node.left = insert(node.left, key);
}else{ //값이 노드보다 큰 경우: 오른쪽 자식으로 이동
node.right = insert(node.right, key);
}
node.height = Math.max(height(node.right), height(node.left))+1; //노드의 높이 업데이트
int balance = getBalance(node); //높이차 계산 -> 균형이 올바른지
//LL을 수행해야하는 경우: 높이차가 1이상 + 키 값이 노드의 왼쪽보다 작은 경우
if(balance > 1 && key < node.left.key){
return rightRotate(node);
}
//RR을 수행해야 하는 경우: 높이차가 -1이하 + 키 값이 노드의 오른쪽보다 큰 경우
if(balance < -1 && key > node.right.key){
return leftRotate(node);
}
//LR을 수행해야 하는 경우: 높이차가 1이상 + 키 값이 왼쪽보다 큰 경우
if(balance > 1 && key > node.left.key){
return lrRotate(node);
}
//RL을 수행해야 하는 경우: 높이차가 -1이하 + 키 값이 오른쪽보다 작은 경우
if(balance < -1 && key < node.right.key){
return rlRotate(node);
}
return node; //균형이 올바르다면 끝
}
//BFS-레벨 순회: (위쪽 레벨부터) 왼쪽 노드 -> 오른쪽 노드
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.print(cur.key+" ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
System.out.println();
}
}(3) 삭제 기능
// 값을 이용해 트리에서 삭제
public void delete(int key){
this.head = delete(this.head, key);
}
// 헤드부터 탐색 시작, 새로 바뀌는 루트 노드를 반환함
private Node delete(Node node, int key){
if(node == null){ //트리가 비어있다면
return null;
}
if(key < node.key){ //현재 노드의 값보다 작을 경우
node.left = delete(node.left, key); //노드의 왼쪽으로 이동
}else if(key > node.key){ //현재 노드의 값보다 클 경우
node.right = delete(node.right, key); //노드의 오른쪽으로 이동
}else{ //현재 노드의 값 == 찾는 값
if(node.left == null){ //현재 노드의 왼쪽 자식이 비어있을 경우
return node.right; //노드의 오른쪽 자식 반환
}else if(node.right == null){ //현재 노드의 오른쪽 자식이 비어있을 경우
return node.left; //노드의 왼쪽 자식 반환
}else{ //둘 다 노드가 존재한다면
Node predecessor = node; //전임자: 현재 노드 (시작)
Node successor = node.left; //후임자: 현재 노드의 왼쪽 자식 (시작)
while(successor.right != null){ //후임자의 오른쪽 노드가 null일 때까지
predecessor = successor; //전임자 <- 후임자
successor = successor.right; //후임자 <- 후임자의 오른쪽 자식
}
predecessor.right = successor.left; //전임자의 오른쪽 자식 <- 후임자의 왼쪽 자식
node.key = successor.key;
}
}
node.height = Math.max(height(node.left), height(node.right))+1;
int balance = getBalance(node);
//LL: 현재 노드의 왼쪽 노드의 높이를 확인하여 LL인지 LR인지 구준
if(balance > 1 && getBalance(node.left) > 0){
return rightRotate(node);
}
//RR
if(balance < -1 && getBalance(node.right) < 0){
return leftRotate(node);
}
//LR
if(balance > 1 && getBalance(node.left) < 0){
return lrRotate(node);
}
//RL
if(balance < -1 && getBalance(node.right) > 0){
return rlRotate(node);
}
return node;
}'자료구조 with JAVA' 카테고리의 다른 글
| [자료구조 with JAVA] 이진 탐색 트리 - Red Black Tree (1) | 2025.03.04 |
|---|---|
| [JAVA] 자료구조 - 이진 탐색 트리 (Binary Search Tree) (0) | 2025.01.07 |
| [JAVA] 자료구조 - 트리 (Tree) (1) | 2024.12.31 |
| [JAVA] 자료구조 - 해시 테이블 (Hash Table) (0) | 2024.12.30 |
| [JAVA] 자료구조 - 데크 (Deque) (0) | 2024.12.30 |